In the field of artificial intelligence, generative models, are based on diffusion models. These in turn are inspired by the world of physics and specifically non-equilibrium thermodynamics, which governs phenomena like the spread of fluids and gases.
Generative models can do something that neural networks have always struggled with; use their training data to generate something new that’s comparable in terms of quality and variety to the original
How it works
Take a simple image made of just two adjacent grayscale pixels. It can be described with two values, based on each pixel’s shade – 0 being completely black to 255 being completely white. These values can be used to plot the image as a point in 2D space. If multiple images are plotted as points, clusters form; certain images and their corresponding pixel values that occur more frequently than others.
On a surface above that 2D plane, where the height of the surface corresponds to how dense the clusters are, a probability distribution is mapped out, with more individual data points underneath the highest part of the surface, and fewer where the surface is lowest. This probability distribution is used to generate new images by randomly generating new data points while adhering to the restriction that more probable data is generated more often. This process is referred to as “sampling” the distribution and each new point is a new image.
For a more realistic million pixel grayscale photograph, that means a million axes, a corresponding probability distribution and resulting million new pixel values to produce an image that resembles the original data set.
With generative modelling, the challenge is to learn this complicated probability distribution and capture extensive information from a set of images that are being used as training data. Once harnessed, though, the fun can begin. Different concepts can be mixed and matched to create new images that were not present in the training data, some of them very surreal indeed.

We have a Stanford academic with an interest in nonequilibrium thermodynamics, systems not in thermal equilibrium that exchange matter and energy internally and with their environment, to thank for all this. His name is Jascha Sohl-Dickstein.
Diffusion and probability distribution
A drop of blue ink diffusing through a container of water first forms a dark blob in one spot. To calculate the probability of finding a molecule of ink in some small volume of the container, a probability distribution must cleanly model the initial state, before the ink begins spreading. This distribution is complex and hard to sample from.
Eventually, the ink diffuses throughout the water, turning it pale blue, leading to a much simpler, more uniform probability distribution of molecules that can be described with a straightforward mathematical expression. Nonequilibrium thermodynamics describes the probability distribution at each step in the diffusion process. Crucially, each step is reversible—with small enough steps, you can go from a simple distribution back to a complex one.
Generative modelling
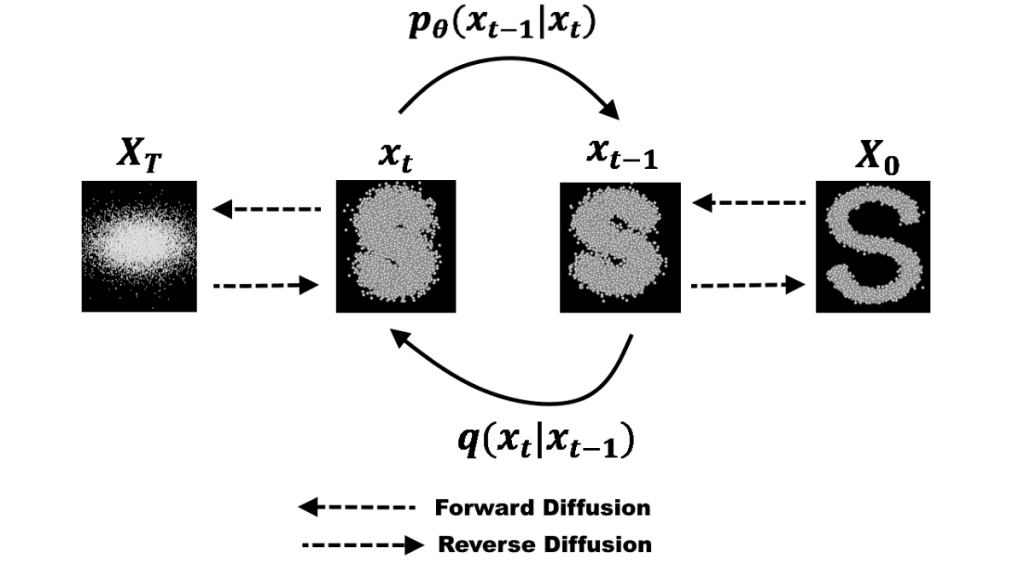
Using the principles of diffusion to develop an algorithm for generative modelling involves first turning complex images in a training data set into simple noise, then teaching the system how to reverse the process, turning noise into images.
Take an image with a million pixels from the training set. Each pixel has a value in a million-dimensional space. The algorithm adds noise to each pixel at every time step – think of how the ink diffuses here. Little by little, the values of the pixels bear less of a relationship to their values in the original image, and the pixels look more like a simple noise distribution. The algorithm also moves each pixel value a little toward the origin, the zero value on all those axes, at each time step. This prevents pixel values from growing too large for computers to easily work with.
Once this process is completed for all images in a data set, an initial complex distribution of dots in million-dimensional space becomes a simple, normal distribution of dots around the origin and results, from the forward pass, in “a big noise ball” and a distribution that can be sampled from with ease.
The machine learning phase
Feed the noisy images obtained from a forward pass into an artificial neural network and train it to predict the less noisy images that came one step earlier. Tweak the parameters of the network to improve the results until it can turn a noisy image that represents a sample from the simple distribution into one that represents a sample from the complex distribution. The trained network is n generative model that no longer needs an original image on which to do a forward pass: The neural network samples directly from a full mathematical description of the simple distribution and converts it into a final image that resembles an image in the training data set. For a full explanation, take a look at the original diffusion model algorithm paper from 2015.
Modern-day diffusion models like DALL·E 2 have their roots in the work of two Stanford academics, Yang Song and Stefano Ermon. Unaware of Jasha Sohl-Dickstein’s work on diffusion models, they published a novel method for building generative models that didn’t estimate the probability distribution of the data (the high-dimensional surface). Instead, estimating the gradient of the distribution (think of it as the slope of the high-dimensional surface).
When increasing levels of noise were added to each image in the training data and the neural network was asked to predict the original image using gradients of the distribution, effectively de-noising it, the model worked better. Once trained, slowly, but achieving excellent results, it could take a noisy image sampled from a simple distribution and progressively turn that back into an image representative of the training data set.
Another academic, Jonathan Ho redesigned and updated Sohl-Dickstein’s diffusion model with some of Song’s ideas and other advances from the world of neural networks, and, with colleagues, announced a new and improved diffusion model in 2020 in a paper titled Denoising Diffusion Probabilistic Models (AKA DDPM). Their models matched or surpassed all competing generative models, including GANs, and their emergence led to the development of DALL·E 2, Stable Diffusion, Imagen and other commercial models, all variants to some degree of DDPM.
Large Language Models
LLMs, generative models trained on text from the internet to learn probability distributions over words instead of images, are a key part of modern diffusion models such as GPT-3. In 2021, an extended team of researchers that included Jonathan Ho showed how to combine information from an LLM and an image-generating diffusion model to use text to guide the process of diffusion and image generation – “guided diffusion” – ushering in tools like DALL·E 2.
Generating Problems
A problem with large language models and diffusion models trained using text and images taken from the Internet is that the results they produce can reflect unwanted biases that reflect society’s ills. Curating and filtering (extremely difficult due to the immensity of the data set), and putting checks on both the input prompts and the outputs of these models., can help.
Mondatum’s CTO Neil Harris leads a team of mathematical programmers, software developers and machine learning specialists. They conduct research and development on behalf of clients to produce new tools that improve technical and creative processes and workflows. For more information on how we can help you in this area, contact Colin Birch – colin@mondatum.com.
Source: Wired
Diffusion model image source: Towards Data Science


